Inference Rule (IR) in DBMS:
- Armstrong's axioms in database management systems were
developed by William w. Armstrong in
1974.
- Armstrong's axioms are the basic
inference rule, used to conclude functional dependencies on a relational
database.
- It provides a set of rules for a
simple reasoning technique in functional dependencies.
- An inference rule is an
assertion that can apply a user on a set of functional dependencies to
derive other FD (functional dependencies).
Inference
rules are divided into major two parts:-
I.
Axioms or
primary rules.
II.
Additional
rules or secondary rules.
I.
Axioms or primary
rules.
1.
Reflexive Rule (IR1)
2.
Augmentation Rule (IR2)
3.
Transitive Rule (IR3)
II.
Additional
rules or secondary rules.
1.
Union Rule (IR4)
2.
Decomposition Rule (IR5)
3.
Pseudo transitive Rule (IR6)
The
Functional dependency has 6 types of inference rules:
1. Reflexive Rule (IR1)
If X is a set of attributes and Y is the subset of X, then X
functionally determines Y.
In the
reflexive rule, if Y is a subset of X, then X determines Y.
1.
If X ⊇ Y then X → Y
Example:
1.
X = {a, b, c, d, e}
- Y = {a, b, c}
2. Augmentation Rule (IR2)
The
augmentation is also called a partial dependency. If X determines Y, then XZ
determines YZ for any Z.
if X determines Y and Z is any attribute set, then XZ determines YZ. It
is also called a partial dependency.
1.
If X → Y then
XZ → YZ
Example:
1.
For R(ABCD), if A → B then AC → BC
3. Transitive Rule (IR3)
In the
transitive rule, if X determines Y and Y determines Z, then X must also
determine Z.
if X determines Y and Y determines Z, then X also determines Z.
1.
If X → Y and Y → Z then X → Z
4. Union Rule (IR4)
This rule is also known as the additive rule. if X determines Y and X
determines Z, then X also determines both Y and Z.
Union rule
says, if X determines Y and X determines Z, then X must also determine Y and Z.
1.
If X → Y and X → Z then X → YZ
Proof:
1. X → Y (given)
2. X → Z (given)
3. X → XY (using IR2 on 1 by augmentation with X. Where XX = X)
4. XY → YZ (using IR2 on 2 by augmentation with Y)
5. X → YZ (using IR3 on 3 and 4)
5. Decomposition Rule (IR5)
This rule is the reverse of the Union rule and is also known as the project rule.
if X determines Y and Z together, then X determines Y and Z separately
1.
If X → YZ then X → Y and X → Z
Proof:
1. X → YZ (given)
2. YZ → Y (using IR1 Rule)
3. X → Y (using IR3 on 1 and 2)
6. Pseudo transitive Rule (IR6)
In the pseudo
transitive rule, if X determines Y, and YZ determines W, then XZ also determines W.
1.
If X → Y and YZ → W then XZ → W
Proof:
1. X → Y (given)
2. WY → Z (given)
3. WX → WY (using IR2 on 1 by augmenting with W)
4. WX → Z (using IR3 on 3 and 2)
========================================================

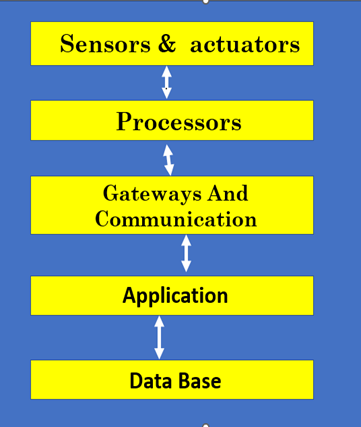
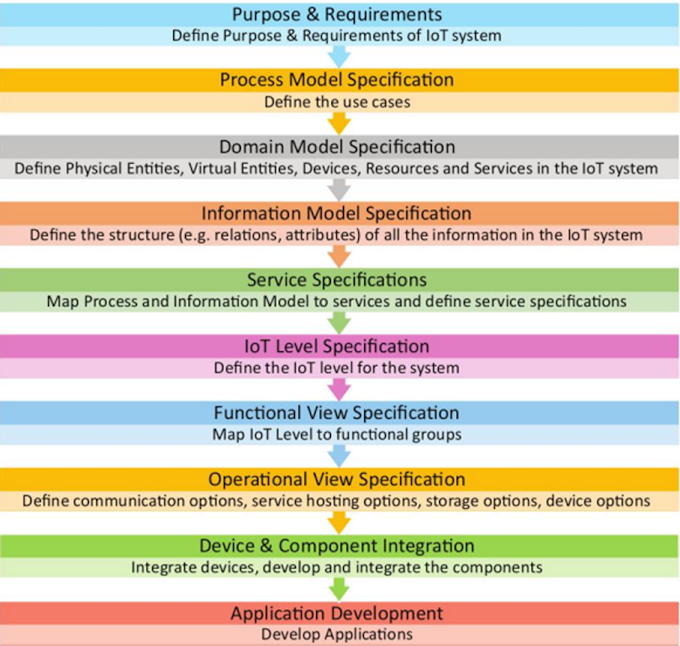
0 Comments